04unsteadyNS.C

Introduction to tutorial 4

In this tutorial we implement a parametrized unsteady Navier-Stokes 2D problem where the parameter is the kinematic viscosity. The physical problem represents an incompressible flow passing around a very long cylinder. The simulation domain is rectangular with spatial bounds of [-4, 30], and [-5, 5] in the X and Y directions, respectively. The cylinder has a radius of 0.5 unit length and is located at the origin. The system has a prescribed uniform inlet velocity of 1 m/s which is constant through the whole simulation.

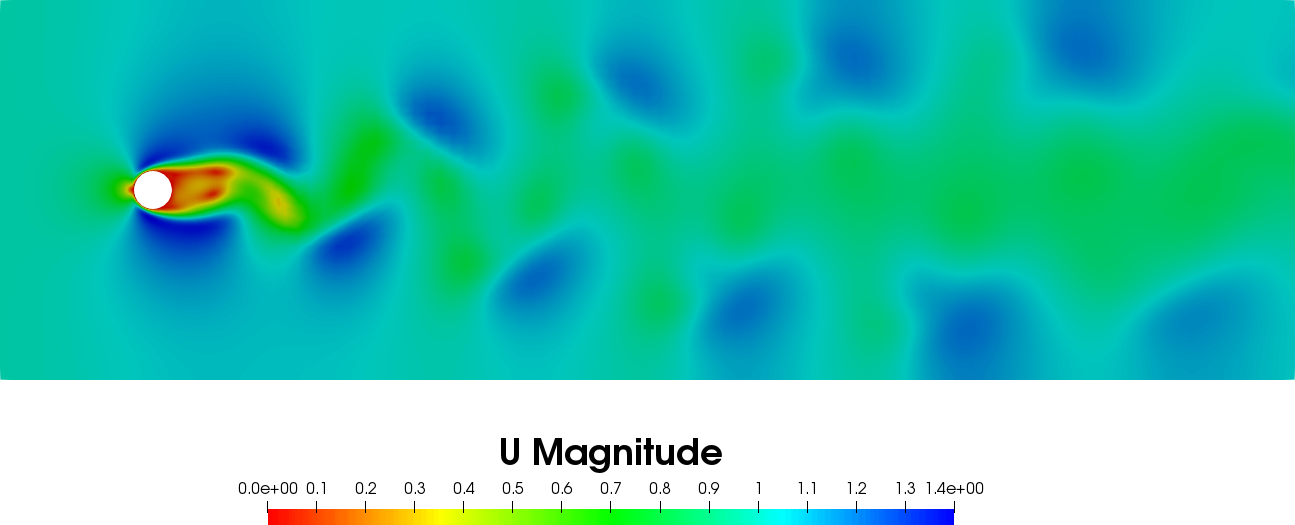
The following image illustrates the simulated system at time = 50 s and Re = 100.

A detailed look into the code

In this section we explain the main steps necessary to construct the tutorial N°4

The necessary header files

First of all let's have a look at the header files that need to be included and what they are responsible for.

The header files of ITHACA-FV necessary for this tutorial are: <unsteadyNS.H> for the full order unsteady NS problem, <ITHACAPOD.H> for the POD decomposition, <reducedUnsteadyNS.H> for the construction of the reduced order problem, and finally <ITHACAstream.H> for some ITHACA input-output operations.

    04unsteadyNS.C
\*---------------------------------------------------------------------------*/
 
#include "unsteadyNS.H"
#include "ITHACAPOD.H"
#include "ReducedUnsteadyNS.H"
#include "ITHACAstream.H"

Definition of the tutorial04 class

We define the tutorial04 class as a child of the unsteadyNS class. The constructor is defined with members that are the fields need to be manipulated during the resolution of the full order problem using pimpleFoam. Such fields are also initialized with the same initial conditions in the solver.

class tutorial04 : public unsteadyNS
{
public:
    explicit tutorial04(int argc, char* argv[])
        : unsteadyNS(argc, argv), U(_U()), p(_p()) {}

Inside the tutorial04 class we define the offlineSolve method according to the specific parametrized problem that needs to be solved. If the offline solve has been previously performed then the method just reads the existing snapshots from the Offline directory. Otherwise it loops over all the parameters, changes the system viscosity with the iterable parameter then performs the offline solve.

    void offlineSolve()
    {
        Vector<double> inl(1, 0, 0);
        List<scalar> mu_now(1);
        label BCind = 0;
 
        if (offline)
        {
            ITHACAstream::read_fields(Ufield, U, "./ITHACAoutput/Offline/");
            ITHACAstream::read_fields(Pfield, p, "./ITHACAoutput/Offline/");
        }
        else
        {
            for (label i = 0; i < mu.cols(); i++)
            {
                mu_now[0] = mu(0, i);
                assignIF(U, inl);
                change_viscosity(mu(0, i));
                truthSolve(mu_now);
            }
        }
    }

We note that in the commented line we show that it is possible to parametrize the boundary conditions. For further details we refer to the classes: reductionProblem, and unsteadyNS.

Definition of the main function

In this section we show the definition of the main function. First we construct the object "example" of type tutorial04:

    tutorial04 example(argc, argv);

Then we parse the ITHACAdict file to determine the number of modes to be written out and also the ones to be used for projection of the velocity, pressure, and the supremizer:

    ITHACAparameters* para = ITHACAparameters::getInstance(example._mesh(), example._runTime());
    int NmodesUout = para->ITHACAdict->lookupOrDefault<int>("NmodesUout", 15);
    int NmodesPout = para->ITHACAdict->lookupOrDefault<int>("NmodesPout", 15);
    int NmodesSUPout = para->ITHACAdict->lookupOrDefault<int>("NmodesSUPout", 15);
    int NmodesUproj = para->ITHACAdict->lookupOrDefault<int>("NmodesUproj", 10);
    int NmodesPproj = para->ITHACAdict->lookupOrDefault<int>("NmodesPproj", 10);
    int NmodesSUPproj = para->ITHACAdict->lookupOrDefault<int>("NmodesSUPproj", 10);

we note that a default value can be assigned in case the parser did not find the corresponding string in the ITHACAdict file.

Now we would like to perform 10 parametrized simulations where the kinematic viscosity is the sole parameter to change, and it lies in the range of {0.1, 0.01} m^2/s equispaced. Alternatively, we can also think of those simulations as that they are performed for fluid flow that has Re changes from Re=10 to Re=100 with step size = 10. In fact, both definitions are the same since the inlet velocity and the domain geometry are both kept fixed through all simulations.

In our implementation, the parameter (viscosity) can be defined by specifying that Nparameters=1, Nsamples=10, and the parameter ranges from 0.1 to 0.01 equispaced, i.e.

    example.Pnumber = 1;
    // Set samples
    example.Tnumber = 1;
    // Set the parameters infos
    example.setParameters();
    // Set the parameter ranges
    example.mu_range(0, 0) = 0.005;
    example.mu_range(0, 1) = 0.005;
    // Generate equispaced samples inside the parameter range
    example.genEquiPar();

After that we set the inlet boundaries where we have the non homogeneous BC:

    example.inletIndex.resize(1, 2);
    example.inletIndex(0, 0) = 0;
    example.inletIndex(0, 1) = 0;

And we set the parameters for the time integration, so as to simulate 20 seconds for each simulation, with a step size = 0.01 seconds, and the data are dumped every 1.0 seconds, i.e.

    example.startTime = 60;
    example.finalTime = 70;
    example.timeStep = 0.01;
    example.writeEvery = 0.1;

Now we are ready to perform the offline stage:

    example.offlineSolve();

and to solve the supremizer problem:

        example.solvesupremizer(); 

In order to search and compute the lifting function (which should be a step function of value equals to the unitary inlet velocity), we perform the following:

Then we create homogenuous basis functions for the velocity:

After that, the modes for velocity, pressure and supremizers are obtained:

then the projection onto the POD modes is performed with:

Now that we obtained all the necessary information from the POD decomposition and the reduced matrices, we are now ready to construct the dynamical system for the reduced order model (ROM). We proceed by constructing the object "reduced" of type reducedUnsteadyNS:

And then we can use the new constructed ROM to perform the online procedure, from which we can simulate the problem at new set of parameters. For instance, we solve the problem with a viscosity=0.055 for a 15 seconds of physical time:

and then the online solve is performed. In this tutorial, the value of the online velocity is in fact a multiplication factor of the step lifting function for the unitary inlet velocity. Therefore the online velocity sets the new BC at the inlet, hence we solve the ROM at new BC.

Finally the ROM solution is reconstructed and exported:

We note that all the previous evaluations of the pressure were based on the supremizers approach. We can also use the Pressure Poisson Equation (PPE) instead of SUP so as to be implemented for the projections, the online solve, and the fields reconstructions.

The plain program

Here there's the plain code

/*---------------------------------------------------------------------------*\
     ██╗████████╗██╗  ██╗ █████╗  ██████╗ █████╗       ███████╗██╗   ██╗
     ██║╚══██╔══╝██║  ██║██╔══██╗██╔════╝██╔══██╗      ██╔════╝██║   ██║
     ██║   ██║   ███████║███████║██║     ███████║█████╗█████╗  ██║   ██║
     ██║   ██║   ██╔══██║██╔══██║██║     ██╔══██║╚════╝██╔══╝  ╚██╗ ██╔╝
     ██║   ██║   ██║  ██║██║  ██║╚██████╗██║  ██║      ██║      ╚████╔╝
     ╚═╝   ╚═╝   ╚═╝  ╚═╝╚═╝  ╚═╝ ╚═════╝╚═╝  ╚═╝      ╚═╝       ╚═══╝
 
 * In real Time Highly Advanced Computational Applications for Finite Volumes
 * Copyright (C) 2017 by the ITHACA-FV authors
-------------------------------------------------------------------------------
License
    This file is part of ITHACA-FV
    ITHACA-FV is free software: you can redistribute it and/or modify
    it under the terms of the GNU Lesser General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version.
    ITHACA-FV is distributed in the hope that it will be useful,
    but WITHOUT ANY WARRANTY; without even the implied warranty of
    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
    GNU Lesser General Public License for more details.
    You should have received a copy of the GNU Lesser General Public License
    along with ITHACA-FV. If not, see <http://www.gnu.org/licenses/>.
Description
    Example of an unsteady NS Reduction Problem
SourceFiles
    04unsteadyNS.C
\*---------------------------------------------------------------------------*/
 
#include "unsteadyNS.H"
#include "ITHACAPOD.H"
#include "ReducedUnsteadyNS.H"
#include "ITHACAstream.H"
#include <chrono>
#include <math.h>
#include <iomanip>
#include <iostream>
 
class tutorial04 : public unsteadyNS
{
public:
    explicit tutorial04(int argc, char* argv[])
        : unsteadyNS(argc, argv), U(_U()), p(_p()) {}
 
    // Fields To Perform
    volVectorField& U;
    volScalarField& p;
 
    void offlineSolve()
    {
        Vector<double> inl(1, 0, 0);
        List<scalar> mu_now(1);
        label BCind = 0;
 
        if (offline)
        {
            ITHACAstream::read_fields(Ufield, U, "./ITHACAoutput/Offline/");
            ITHACAstream::read_fields(Pfield, p, "./ITHACAoutput/Offline/");
        }
        else
        {
            for (label i = 0; i < mu.cols(); i++)
            {
                mu_now[0] = mu(0, i);
                assignIF(U, inl);
                change_viscosity(mu(0, i));
                truthSolve(mu_now);
            }
        }
    }
};
 
/*---------------------------------------------------------------------------*\
                               Starting the MAIN
\*---------------------------------------------------------------------------*/
int main(int argc, char* argv[])
{
    // Construct the tutorial04 object
    tutorial04 example(argc, argv);
 
    // Read parameters from ITHACAdict file
    ITHACAparameters* para = ITHACAparameters::getInstance(example._mesh(), example._runTime());
    int NmodesUout = para->ITHACAdict->lookupOrDefault<int>("NmodesUout", 15);
    int NmodesPout = para->ITHACAdict->lookupOrDefault<int>("NmodesPout", 15);
    int NmodesSUPout = para->ITHACAdict->lookupOrDefault<int>("NmodesSUPout", 15);
    int NmodesUproj = para->ITHACAdict->lookupOrDefault<int>("NmodesUproj", 10);
    int NmodesPproj = para->ITHACAdict->lookupOrDefault<int>("NmodesPproj", 10);
    int NmodesSUPproj = para->ITHACAdict->lookupOrDefault<int>("NmodesSUPproj", 10);
 
    // Set the number of parameters
    example.Pnumber = 1;
    // Set samples
    example.Tnumber = 1;
    // Set the parameters infos
    example.setParameters();
    // Set the parameter ranges
    example.mu_range(0, 0) = 0.005;
    example.mu_range(0, 1) = 0.005;
    // Generate equispaced samples inside the parameter range
    example.genEquiPar();
    // Set the inlet boundaries where we have non homogeneous boundary conditions
    example.inletIndex.resize(1, 2);
    example.inletIndex(0, 0) = 0;
    example.inletIndex(0, 1) = 0;
    // Time parameters
    example.startTime = 60;
    example.finalTime = 70;
    example.timeStep = 0.01;
    example.writeEvery = 0.1;
    // Perform The Offline Solve
    example.offlineSolve();
 
    // Check if lift or penalty method should be used
    if (example.bcMethod == "lift")
    {
        // Search the lift function
        example.liftSolve();
        // Normalize the lifting function
        ITHACAutilities::normalizeFields(example.liftfield);
        // Create homogeneous basis functions for velocity
        example.computeLift(example.Ufield, example.liftfield, example.Uomfield);
        // Perform a POD decomposition for velocity and pressure
        ITHACAPOD::getModes(example.Uomfield, example.Umodes, example._U().name(), example.podex, 0, 0, NmodesUout);
        ITHACAPOD::getModes(example.Pfield, example.Pmodes, example._p().name(), example.podex, 0, 0, NmodesPout);
    }
    else
    {
        // Perform a POD decomposition for velocity and pressure without lifting function
        ITHACAPOD::getModes(example.Ufield, example.Umodes, example._U().name(), example.podex, 0, 0, NmodesUout);
        ITHACAPOD::getModes(example.Pfield, example.Pmodes, example._p().name(), example.podex, 0, 0, NmodesPout);
    }
    // Check the method and perform the appropriate projection
    if (example.method == "supremizer")
    {
        example.solvesupremizer(); 
        ITHACAPOD::getModes(example.supfield, example.supmodes, example._U().name(), example.podex, example.supex, 1, NmodesSUPout);
        example.projectSUP("./Matrices", NmodesUproj, NmodesPproj, NmodesSUPproj);
    }
    else if (example.method == "PPE")
    {
        example.projectPPE("./Matrices", NmodesUproj, NmodesPproj);
    }
 
    reducedUnsteadyNS reduced(example);
 
    // Set values of the reduced stuff
    reduced.nu = 0.005;
    reduced.tstart = 60;
    reduced.finalTime = 70;
    reduced.dt = 0.005;
    reduced.storeEvery = 0.005;
    reduced.exportEvery = 0.1;
 
    // Set the online velocity
    Eigen::MatrixXd vel_now(1, 1);
    vel_now(0, 0) = 1;
 
    // If using the penalty method, set tauU
    if (example.bcMethod == "penalty")
    {
        reduced.tauU = Eigen::MatrixXd::Zero(1, 1);
        reduced.tauU(0, 0) = 1e-1;  // Example penalty coefficient
    }
 
    // Perform the online solve based on the method
    if (example.method == "supremizer")
    {
        reduced.solveOnline_sup(vel_now, 1);
    }
    else if (example.method == "PPE")
    {
        reduced.solveOnline_PPE(vel_now, 1);
    }
 
    // Reconstruct the solution and export it
    reduced.reconstruct(true, "./ITHACAoutput/Reconstruction" + example.method + "/");
 
    exit(0);
}