08DEIM.C

Introduction to tutorial 8

In this tutorial we propose an example concerning the usage of the Discrete Empirical Interpolation Method (implemented in the HyperReduction class) for the approximation of a non-linear function. The following image illustrates the computational domain used to discretize the problem

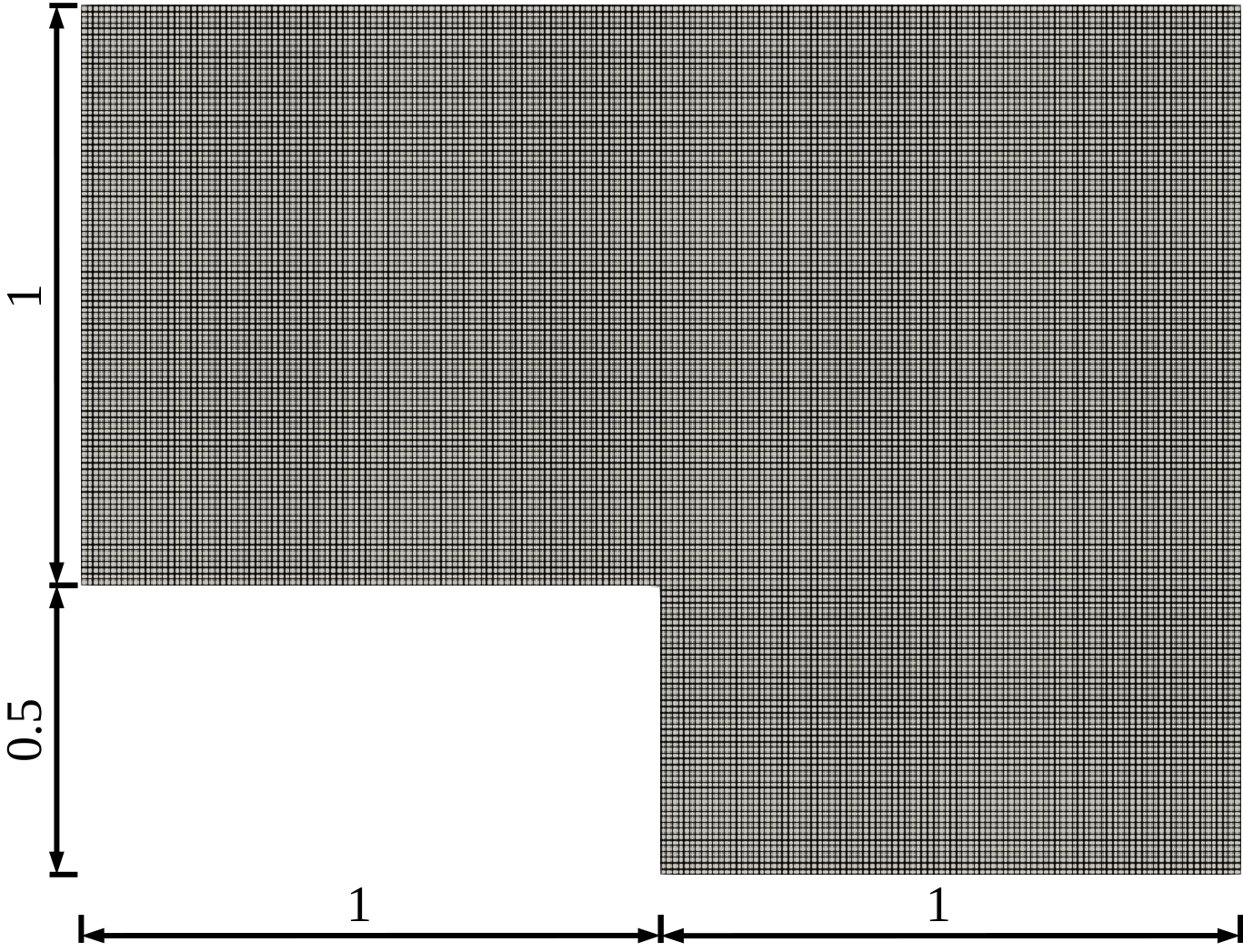
Computational Domain

The non-linear function is described by a parametric Gaussian function:

\[ S(\mathbf{x},\mathbf{\mu}) = e^{-2(x-\mu_x-1)^2 - 2(y-\mu_y-0.5)^2}, \]

that is depending on the parameter vector \(\mathbf{\mu} = [\mu_x, \mu_y] \) and on the location inside the domain \( \mathbf{x} = [x,y] \). A training set of 100 samples is used to construct the "DEIM" modes which are later used for the approximation.

The necessary header files

First of all let's have a look to the header files that needs to be included and what they are responsible for: The header files of ITHACA-FV necessary for this tutorial are: <Foam2Eigen.H> for Eigen to OpenFOAM conversion of objects, <ITHACAstream.H> for ITHACA-FV input-output operations. <ITHACAPOD.H> for the POD decomposition, <hyperReduction.templates.H> for the "DEIM" approximation.

A detailed look into the code

The OpenFOAM header files:

#include "fvCFD.H"
#include "fvOptions.H"
#include "simpleControl.H"
#include "simpleControl.H"
#include "fvMeshSubset.H"

ITHACA-FV header files

#include "ITHACAutilities.H"
#include "Foam2Eigen.H"
#include "ITHACAstream.H"
#include "ITHACAPOD.H"
#include "hyperReduction.templates.H"

chrono to compute the speedup

#include <chrono>

Construction of the function to be approximated with the "DEIM" method from the HyperReduction class.

class DEIM_function : public HyperReduction<PtrList<volScalarField>&>
{
    public:
        using HyperReduction::HyperReduction;

Method with the explicit definition of the non-linear function

        static volScalarField evaluate_expression(volScalarField& S, Eigen::MatrixXd mu)
        {
            volScalarField yPos = S.mesh().C().component(vector::Y).ref();
            volScalarField xPos = S.mesh().C().component(vector::X).ref();
 
            for (auto i = 0; i < S.size(); i++)
            {
                S[i] = std::exp( - 2 * std::pow(xPos[i] - mu(0) - 1,
                                                2) - 2 * std::pow(yPos[i] - mu(1) - 0.5, 2));
            }
 
            return S;
        }

Method with the expression for the evaluation of the online coefficients

        Eigen::VectorXd onlineCoeffs(Eigen::MatrixXd mu)
        {
            theta.resize(nodePoints().size());
            auto f = evaluate_expression(subField(), mu);
 
            for (int i = 0; i < nodePoints().size(); i++)
            {
                // double on_coeff = f[localMagicPoints[i]];
                theta(i) = f[localNodePoints[i]];
            }
 
            return theta;
        }

Now let's have a look to important command in the main function. Read parameters from the ITHACAdict file

    ITHACAparameters* para = ITHACAparameters::getInstance(mesh, runTime);
    int NDEIM = para->ITHACAdict->lookupOrDefault<int>("NDEIM", 15);

Definition of the parameter samples to train the non-linear function

    Eigen::MatrixXd pars = ITHACAutilities::rand(100, 2, -0.5, 0.5);

Offline training of the function and assembly of the snapshots list

    // Perform the offline phase
    for (int i = 0; i < 100; i++)
    {
        DEIM_function::evaluate_expression(S, pars.row(i));
        Sp.append((S).clone());
        ITHACAstream::exportSolution(S, name(i + 1), "./ITHACAoutput/Offline/");
    }

Compute the "DEIM" modes using the ITHACAPOD class

    Eigen::VectorXd normalizingWeights = ITHACAutilities::getMassMatrixFV(Sp[0]).array();
    PtrList<volScalarField> modes = ITHACAPOD::DEIMmodes(Sp, NDEIM, "GappyDEIM", S.name());
    snapshotsModes = Foam2Eigen::PtrList2Eigen(modes);

Construction of the HyperReduction object passing the maximum number of "DEIM" modes NDEIM, the initSeeds (none in this tutorial), the name used to store the output "DEIM" and the list of snapshots Sp. The constructor is taking the number of modes and the number of point to compute, for the "DEIM" method these numbers are equal.

    Eigen::VectorXi initSeeds(0);
    DEIM_function c(NDEIM, NDEIM, initSeeds, "DEIM", Sp);

Compute the "DEIM" method HyperReduction::offlineGappyDEIM passing the "DEIM" modes and the normalizingWeights

    c.offlineGappyDEIM(snapshotsModes, normalizingWeights);

Command to generate the submeshes used for pointwise evaluation of the function

    c.generateSubmesh(2, mesh); 
    c.subField = c.interpolateField<volScalarField>(Sp[0]);

Definition of a new sample value to test the accuracy of the method \( \mu* = (0,0) \)

    Eigen::MatrixXd par_new(2, 1);
    par_new(0, 0) = 0;
    par_new(1, 0) = 0;

Evaluation of the function using "DEIM" and reconstruction of the field

    Eigen::VectorXd aprfield = c.MatrixOnline * c.onlineCoeffs(par_new);
    // Transform to an OpenFOAM field and export
    volScalarField S2("S_online", Foam2Eigen::Eigen2field(S, aprfield));

Export the approximation

    ITHACAstream::exportSolution(S2, name(1), "./ITHACAoutput/Online/");

Evaluate the function on in \(\mu*\) using the FOM

    DEIM_function::evaluate_expression(S, par_new);

Export the FOM field

    ITHACAstream::exportSolution(S, name(1), "./ITHACAoutput/Online/");

Compute the error and print it

    Info << ITHACAutilities::errorL2Rel(S2, S) << endl;

The plain program

Here there's the plain code

/*---------------------------------------------------------------------------*\
     ██╗████████╗██╗  ██╗ █████╗  ██████╗ █████╗       ███████╗██╗   ██╗
     ██║╚══██╔══╝██║  ██║██╔══██╗██╔════╝██╔══██╗      ██╔════╝██║   ██║
     ██║   ██║   ███████║███████║██║     ███████║█████╗█████╗  ██║   ██║
     ██║   ██║   ██╔══██║██╔══██║██║     ██╔══██║╚════╝██╔══╝  ╚██╗ ██╔╝
     ██║   ██║   ██║  ██║██║  ██║╚██████╗██║  ██║      ██║      ╚████╔╝
     ╚═╝   ╚═╝   ╚═╝  ╚═╝╚═╝  ╚═╝ ╚═════╝╚═╝  ╚═╝      ╚═╝       ╚═══╝
 
 * In real Time Highly Advanced Computational Applications for Finite Volumes
 * Copyright (C) 2017 by the ITHACA-FV authors
-------------------------------------------------------------------------------
License
    This file is part of ITHACA-FV
    ITHACA-FV is free software: you can redistribute it and/or modify
    it under the terms of the GNU Lesser General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version.
    ITHACA-FV is distributed in the hope that it will be useful,
    but WITHOUT ANY WARRANTY; without even the implied warranty of
    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
    GNU Lesser General Public License for more details.
    You should have received a copy of the GNU Lesser General Public License
    along with ITHACA-FV. If not, see <http://www.gnu.org/licenses/>.
Description
    Example of the reconstruction of a non-linear function using the DEIM
SourceFiles
    08DEIM.C
\*---------------------------------------------------------------------------*/
 
#include "fvCFD.H"
#include "fvOptions.H"
#include "simpleControl.H"
#include "simpleControl.H"
#include "fvMeshSubset.H"
#include "ITHACAutilities.H"
#include "Foam2Eigen.H"
#include "ITHACAstream.H"
#include "ITHACAPOD.H"
#include "hyperReduction.templates.H"
#include <chrono>
class DEIM_function : public HyperReduction<PtrList<volScalarField>&>
{
    public:
        using HyperReduction::HyperReduction;
        static volScalarField evaluate_expression(volScalarField& S, Eigen::MatrixXd mu)
        {
            volScalarField yPos = S.mesh().C().component(vector::Y).ref();
            volScalarField xPos = S.mesh().C().component(vector::X).ref();
 
            for (auto i = 0; i < S.size(); i++)
            {
                S[i] = std::exp( - 2 * std::pow(xPos[i] - mu(0) - 1,
                                                2) - 2 * std::pow(yPos[i] - mu(1) - 0.5, 2));
            }
 
            return S;
        }
        Eigen::VectorXd onlineCoeffs(Eigen::MatrixXd mu)
        {
            theta.resize(nodePoints().size());
            auto f = evaluate_expression(subField(), mu);
 
            for (int i = 0; i < nodePoints().size(); i++)
            {
                // double on_coeff = f[localMagicPoints[i]];
                theta(i) = f[localNodePoints[i]];
            }
 
            return theta;
        }
        
        Eigen::VectorXd theta; 
        PtrList<volScalarField> fields;
        autoPtr<volScalarField> subField;
};
 
int main(int argc, char* argv[])
{
    // Read parameters from ITHACAdict file
#include "setRootCase.H"
    Foam::Time runTime(Foam::Time::controlDictName, args);
    Foam::fvMesh mesh
    (
        Foam::IOobject
        (
            Foam::fvMesh::defaultRegion,
            runTime.timeName(),
            runTime,
            Foam::IOobject::MUST_READ
        )
    );
    ITHACAparameters* para = ITHACAparameters::getInstance(mesh, runTime);
    int NDEIM = para->ITHACAdict->lookupOrDefault<int>("NDEIM", 15);
    simpleControl simple(mesh);
#include "createFields.H"
    // List of volScalarField where the snapshots are stored
    PtrList<volScalarField> Sp;
    // Non linear function
    volScalarField S
    (
        IOobject
        (
            "S",
            runTime.timeName(),
            mesh,
            IOobject::NO_READ,
            IOobject::AUTO_WRITE
        ),
        T.mesh(),
        dimensionedScalar("zero", dimensionSet(0, 0, -1, 1, 0, 0, 0), 0)
    );
    // Parameters used to train the non-linear function
    Eigen::MatrixXd pars = ITHACAutilities::rand(100, 2, -0.5, 0.5);
    
    // To compare with the same parameters, save data and then load it 
    // cnpy::load(pars, "./random100.npy");
    // cnpy::save(pars, "./random100.npy");
 
    // Perform the offline phase
    for (int i = 0; i < 100; i++)
    {
        DEIM_function::evaluate_expression(S, pars.row(i));
        Sp.append((S).clone());
        ITHACAstream::exportSolution(S, name(i + 1), "./ITHACAoutput/Offline/");
    }
 
    Eigen::MatrixXd snapshotsModes;
 
    // To use the DEIMmodes method from ITHACAPOD :
    Eigen::VectorXd normalizingWeights = ITHACAutilities::getMassMatrixFV(Sp[0]).array();
    PtrList<volScalarField> modes = ITHACAPOD::DEIMmodes(Sp, NDEIM, "GappyDEIM", S.name());
    snapshotsModes = Foam2Eigen::PtrList2Eigen(modes);
 
    // To use the SVD modes from the HyperReduction class : 
    // Eigen::VectorXd normalizingWeights;
    // c.getModesSVD(c.snapshotsListTuple, snapshotsModes, normalizingWeights); 
 
    // Create DEIM object with given number of basis functions
    Eigen::VectorXi initSeeds(0);
    DEIM_function c(NDEIM, NDEIM, initSeeds, "DEIM", Sp);
 
    // Compute the DEIM 
    c.offlineGappyDEIM(snapshotsModes, normalizingWeights);
    // To access the same folder hierarchy as before : 
    // c.problemName = "Gaussian_function";
    // c.offlineGappyDEIM(snapshotsModes, normalizingWeights, "ITHACAoutput/DEIM/"+c.problemName);
                                                           
    // Generate the submeshes with the depth of the layer
    c.generateSubmesh(2, mesh); 
    c.subField = c.interpolateField<volScalarField>(Sp[0]);
 
    // Define a new online parameter
    Eigen::MatrixXd par_new(2, 1);
    par_new(0, 0) = 0;
    par_new(1, 0) = 0;
    // Online evaluation of the non linear function
    Eigen::VectorXd aprfield = c.MatrixOnline * c.onlineCoeffs(par_new);
    // Transform to an OpenFOAM field and export
    volScalarField S2("S_online", Foam2Eigen::Eigen2field(S, aprfield));
    ITHACAstream::exportSolution(S2, name(1), "./ITHACAoutput/Online/");
    // Evaluate the full order function and export it
    DEIM_function::evaluate_expression(S, par_new);
    ITHACAstream::exportSolution(S, name(1), "./ITHACAoutput/Online/");
    // Compute the L2 error and print it
    Info << ITHACAutilities::errorL2Rel(S2, S) << endl;
    return 0;
}