02thermalBlock.C

Introduction to tutorial 2

The problems consists of a thermal block with a source term. The problem equations are:

\[ \nabla \cdot (k \nabla T) = S \]

where \(k\) is the diffusivity, \(T\) is the temperature and \(S\) is the source term. The problem discretised and formalized in matrix equation reads:

\[ AT = S \]

where \(A\) is the matrix of interpolation coefficients, \(T\) is the vector of unknowns and \(S\) is the vector representing the source term. The domain is subdivided in 9 different parts and each part has parametrized diffusivity. See the image below for a clarification.

Both the full order and the reduced order problem are solved exploiting the parametric affine decomposition of the differential operators:

\[ A = \sum_{i=1}^N \theta_i(\mu) A_i \]

For the operations performed by each command check the comments in the source 02thermalBlock.C file.

The ITHACAPODdict file

In this section are explained the main steps necessary to construct the tutorial N°2

The necessary header files

First of all let's have a look to the header files that needs to be included and what they are responsible for:

The standard C++ header for input/output stream objects:

#include <iostream>

The OpenFOAM header files:

#include "fvCFD.H"
#include "IOmanip.H"
#include "Time.H"

The header file of ITHACA-FV necessary for this tutorial

#include "ITHACAPOD.H"
#include "ITHACAutilities.H"

The Eigen library for matrix manipulation and linear and non-linear algebra operations:

#include <Eigen/Dense>

And we define some mathematical constants and include the standard header for common math operations:

#define _USE_MATH_DEFINES
#include <cmath>

Implementation of the tutorial02 class

Then we can define the tutorial02 class as a child of the laplacianProblem class

class tutorial02: public laplacianProblem
{
    public:
        explicit tutorial02(int argc, char* argv[])
            :
            laplacianProblem(argc, argv),
            T(_T()),
            nu(_nu()),
            S(_S())
        {}

The members of the class are the fields that needs to be manipulated during the resolution of the problem

Inside the class it is defined the offline solve method according to the specific parametrized problem that needs to be solved.

        void offlineSolve(word folder = "./ITHACAoutput/Offline/")
        {

If the offline solve has already been performed than read the existing snapshots

            if (offline)
            {
                ITHACAstream::read_fields(Tfield, "T", folder);
                mu_samples =
                    ITHACAstream::readMatrix(folder + "/mu_samples_mat.txt");
            }

else perform the offline solve where a loop over all the parameters is performed:

                for (label i = 0; i < mu.rows(); i++)
                {
                    for (label j = 0; j < mu.cols() ; j++)
                    {
                        // mu_now[i] =
                        theta[j] = mu(i, j);
                    }

a 0 internal constant value is assigned before each solve command with the lines

                    assignIF(T, IF);

and the solve operation is performed, see also the laplacianProblem class for the definition of the methods

                    truthSolve(mu_now, folder);

The we need also to implement a method to set/define the source term that may be problem dependent. In this case the source term is defined with a hat function:

        void SetSource()
        {
            volScalarField yPos = T.mesh().C().component(vector::Y).ref();
            volScalarField xPos = T.mesh().C().component(vector::X).ref();
            forAll(S, counter)
            {
                S[counter] = Foam::sin(xPos[counter] / 0.9 * M_PI) + Foam::sin(
                                 yPos[counter] / 0.9 * M_PI);
            }
        }

Define by:

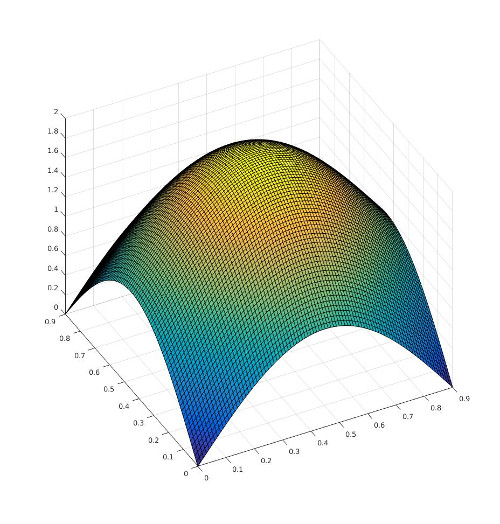
\[ S = \sin(\frac{\pi}{L}\cdot x) + \sin(\frac{\pi}{L}\cdot y) \]

where \(L\) is the dimension of the thermal block which is equal to 0.9.

With the following is defined a method to set compute the parameter of the affine expansion:

        void compute_nu()
        {

The list of parameters is resized according to number of parametrized regions

            nu_list.resize(9);

The nine different volScalarFields to identify the viscosity in each domain are initialized:

            volScalarField nu1(nu);
            volScalarField nu2(nu);
            volScalarField nu3(nu);
            volScalarField nu4(nu);
            volScalarField nu5(nu);
            volScalarField nu6(nu);
            volScalarField nu7(nu);
            volScalarField nu8(nu);
            volScalarField nu9(nu);

and the 9 different boxes are defined:

            Eigen::MatrixXd Box1(2, 3);
            Box1 << 0, 0, 0, 0.3, 0.3, 0.1;
            Eigen::MatrixXd Box2(2, 3);
            Box2 << 0.3, 0, 0, 0.6, 0.3, 0.1;
            Eigen::MatrixXd Box3(2, 3);
            Box3 << 0.6, 0, 0, 0.91, 0.3, 0.1;
            Eigen::MatrixXd Box4(2, 3);
            Box4 << 0, 0.3, 0, 0.3, 0.6, 0.1;
            Eigen::MatrixXd Box5(2, 3);
            Box5 << 0.3, 0.3, 0, 0.6, 0.6, 0.1;
            Eigen::MatrixXd Box6(2, 3);
            Box6 << 0.6, 0.3, 0, 0.91, 0.6, 0.1;
            Eigen::MatrixXd Box7(2, 3);
            Box7 << 0, 0.6, 0, 0.3, 0.91, 0.1;
            Eigen::MatrixXd Box8(2, 3);
            Box8 << 0.3, 0.61, 0, 0.6, 0.91, 0.1;
            Eigen::MatrixXd Box9(2, 3);

and for each of the defined boxes the relative diffusivity field is set to 1 inside the box and remain 0 elsewhere:

            ITHACAutilities::setBoxToValue(nu1, Box1, 1.0);
            ITHACAutilities::setBoxToValue(nu2, Box2, 1.0);
            ITHACAutilities::setBoxToValue(nu3, Box3, 1.0);
            ITHACAutilities::setBoxToValue(nu4, Box4, 1.0);
            ITHACAutilities::setBoxToValue(nu5, Box5, 1.0);
            ITHACAutilities::setBoxToValue(nu6, Box6, 1.0);
            ITHACAutilities::setBoxToValue(nu7, Box7, 1.0);
            ITHACAutilities::setBoxToValue(nu8, Box8, 1.0);
            ITHACAutilities::setBoxToValue(nu9, Box9, 1.0);

See also the ITHACAutilities::setBoxToValue for more details.

The list of diffusivity fields is set with:

            nu_list.set(0, (nu1).clone());
            nu_list.set(1, (nu2).clone());
            nu_list.set(2, (nu3).clone());
            nu_list.set(3, (nu4).clone());
            nu_list.set(4, (nu5).clone());
            nu_list.set(5, (nu6).clone());
            nu_list.set(6, (nu7).clone());
            nu_list.set(7, (nu8).clone());
            nu_list.set(8, (nu9).clone());
        }

Definition of the main function

Once the tutorial02 class is defined the main function is defined, an example of type tutorial02 is constructed:

    tutorial02 example(argc, argv);

the number of parameter is set:

    example.Pnumber = 9;
    example.setParameters();

the range of the parameters is defined:

    example.mu_range.col(0) = Eigen::MatrixXd::Ones(9, 1) * 0.001;
    example.mu_range.col(1) = Eigen::MatrixXd::Ones(9, 1) * 0.1;

and 500 random combinations of the parameters are generated:

    example.genRandPar(500);

the size of the list of values that are multiplying the affine forms is set:

    example.theta.resize(9);

the source term is defined, the compute_nu and assemble_operator functions are called

    example.SetSource();
    example.compute_nu();
    example.assemble_operator();

then the Offline full order Solve is performed:

    example.offlineSolve();

Once the Offline solve is performed the modes ar obtained using the ITHACAPOD::getModes function:

    ITHACAPOD::getModes(example.Tfield, example.Tmodes, example._T().name(),

and the projection is performed onto the POD modes using 10 modes

    example.project(NmodesTproj);

Once the projection is performed we can construct a reduced object:

    reducedLaplacian reduced(example);

and solve the reduced problem for some values of the parameters:

    for (int i = 0; i < FOM_test.mu.rows(); i++)
    {
        reduced.solveOnline(FOM_test.mu.row(i));
    }

Finally, once the online solve has been performed we can reconstruct the solution:

    reduced.reconstruct("./ITHACAoutput/Reconstruction");

The plain program

Here there's the plain code

/*---------------------------------------------------------------------------*\
     ██╗████████╗██╗  ██╗ █████╗  ██████╗ █████╗       ███████╗██╗   ██╗
     ██║╚══██╔══╝██║  ██║██╔══██╗██╔════╝██╔══██╗      ██╔════╝██║   ██║
     ██║   ██║   ███████║███████║██║     ███████║█████╗█████╗  ██║   ██║
     ██║   ██║   ██╔══██║██╔══██║██║     ██╔══██║╚════╝██╔══╝  ╚██╗ ██╔╝
     ██║   ██║   ██║  ██║██║  ██║╚██████╗██║  ██║      ██║      ╚████╔╝
     ╚═╝   ╚═╝   ╚═╝  ╚═╝╚═╝  ╚═╝ ╚═════╝╚═╝  ╚═╝      ╚═╝       ╚═══╝
 
 * In real Time Highly Advanced Computational Applications for Finite Volumes
 * Copyright (C) 2017 by the ITHACA-FV authors
-------------------------------------------------------------------------------
License
    This file is part of ITHACA-FV
    ITHACA-FV is free software: you can redistribute it and/or modify
    it under the terms of the GNU Lesser General Public License as published by
    the Free Software Foundation, either version 3 of the License, or
    (at your option) any later version.
    ITHACA-FV is distributed in the hope that it will be useful,
    but WITHOUT ANY WARRANTY; without even the implied warranty of
    MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
    GNU Lesser General Public License for more details.
    You should have received a copy of the GNU Lesser General Public License
    along with ITHACA-FV. If not, see <http://www.gnu.org/licenses/>.
Description
    Example of a heat transfer Reduction Problem
SourceFiles
    02thermalBlock.C
\*---------------------------------------------------------------------------*/
 
#include <iostream>
#include "fvCFD.H"
#include "IOmanip.H"
#include "Time.H"
#include "laplacianProblem.H"
#include "ReducedLaplacian.H"
#include "ITHACAPOD.H"
#include "ITHACAutilities.H"
#include <Eigen/Dense>
#define _USE_MATH_DEFINES
#include <cmath>
 
class tutorial02: public laplacianProblem
{
    public:
        explicit tutorial02(int argc, char* argv[])
            :
            laplacianProblem(argc, argv),
            T(_T()),
            nu(_nu()),
            S(_S())
        {}
        volScalarField& T;
        volScalarField& nu;
        volScalarField& S;
 
        void offlineSolve(word folder = "./ITHACAoutput/Offline/")
        {
            if (offline)
            {
                ITHACAstream::read_fields(Tfield, "T", folder);
                mu_samples =
                    ITHACAstream::readMatrix(folder + "/mu_samples_mat.txt");
            }
            else
            {
                List<scalar> mu_now(9);
                scalar IF = 0;
 
                for (label i = 0; i < mu.rows(); i++)
                {
                    for (label j = 0; j < mu.cols() ; j++)
                    {
                        // mu_now[i] =
                        theta[j] = mu(i, j);
                    }
 
                    assignIF(T, IF);
                    Info << i << endl;
                    truthSolve(mu_now, folder);
                }
            }
        }
 
        void SetSource()
        {
            volScalarField yPos = T.mesh().C().component(vector::Y).ref();
            volScalarField xPos = T.mesh().C().component(vector::X).ref();
            forAll(S, counter)
            {
                S[counter] = Foam::sin(xPos[counter] / 0.9 * M_PI) + Foam::sin(
                                 yPos[counter] / 0.9 * M_PI);
            }
        }
 
        void compute_nu()
        {
            nu_list.resize(9);
            volScalarField nu1(nu);
            volScalarField nu2(nu);
            volScalarField nu3(nu);
            volScalarField nu4(nu);
            volScalarField nu5(nu);
            volScalarField nu6(nu);
            volScalarField nu7(nu);
            volScalarField nu8(nu);
            volScalarField nu9(nu);
            Eigen::MatrixXd Box1(2, 3);
            Box1 << 0, 0, 0, 0.3, 0.3, 0.1;
            Eigen::MatrixXd Box2(2, 3);
            Box2 << 0.3, 0, 0, 0.6, 0.3, 0.1;
            Eigen::MatrixXd Box3(2, 3);
            Box3 << 0.6, 0, 0, 0.91, 0.3, 0.1;
            Eigen::MatrixXd Box4(2, 3);
            Box4 << 0, 0.3, 0, 0.3, 0.6, 0.1;
            Eigen::MatrixXd Box5(2, 3);
            Box5 << 0.3, 0.3, 0, 0.6, 0.6, 0.1;
            Eigen::MatrixXd Box6(2, 3);
            Box6 << 0.6, 0.3, 0, 0.91, 0.6, 0.1;
            Eigen::MatrixXd Box7(2, 3);
            Box7 << 0, 0.6, 0, 0.3, 0.91, 0.1;
            Eigen::MatrixXd Box8(2, 3);
            Box8 << 0.3, 0.61, 0, 0.6, 0.91, 0.1;
            Eigen::MatrixXd Box9(2, 3);
            Box9 << 0.6, 0.6, 0, 0.9, 0.91, 0.1;
            ITHACAutilities::setBoxToValue(nu1, Box1, 1.0);
            ITHACAutilities::setBoxToValue(nu2, Box2, 1.0);
            ITHACAutilities::setBoxToValue(nu3, Box3, 1.0);
            ITHACAutilities::setBoxToValue(nu4, Box4, 1.0);
            ITHACAutilities::setBoxToValue(nu5, Box5, 1.0);
            ITHACAutilities::setBoxToValue(nu6, Box6, 1.0);
            ITHACAutilities::setBoxToValue(nu7, Box7, 1.0);
            ITHACAutilities::setBoxToValue(nu8, Box8, 1.0);
            ITHACAutilities::setBoxToValue(nu9, Box9, 1.0);
            nu_list.set(0, (nu1).clone());
            nu_list.set(1, (nu2).clone());
            nu_list.set(2, (nu3).clone());
            nu_list.set(3, (nu4).clone());
            nu_list.set(4, (nu5).clone());
            nu_list.set(5, (nu6).clone());
            nu_list.set(6, (nu7).clone());
            nu_list.set(7, (nu8).clone());
            nu_list.set(8, (nu9).clone());
        }
 
        void assemble_operator()
        {
            for (int i = 0; i < nu_list.size(); i++)
            {
                operator_list.append(fvm::laplacian(nu_list[i], T));
            }
        }
 
};
 
void offline_stage(tutorial02& example, tutorial02& FOM_test);
void online_stage(tutorial02& example, tutorial02& FOM_test);
 
int main(int argc, char* argv[])
{
#if OPENFOAM > 1812
    // load stage to perform
    argList::addOption("stage", "offline", "Perform offline stage");
    argList::addOption("stage", "online", "Perform online stage");
    // add options for parallel run
    HashTable<string> validParOptions;
    validParOptions.set
    (
        "stage",
        "offline"
    );
    validParOptions.set
    (
        "stage",
        "online"
    );
    Pstream::addValidParOptions(validParOptions);
    // Construct the tutorial object
    tutorial02 example(argc, argv);
    tutorial02 FOM_test(argc, argv);
 
    if (example._args().get("stage").match("offline"))
    {
        // perform the offline stage, extracting the modes from the snapshots'
        // dataset corresponding to parOffline
        offline_stage(example, FOM_test);
    }
    else if (example._args().get("stage").match("online"))
    {
        // load precomputed modes and reduced matrices
        offline_stage(example, FOM_test);
        // perform online solve with respect to the parameters in parOnline
        online_stage(example, FOM_test);
    }
    else
    {
        Info << "Pass '-stage offline', '-stage online'" << endl;
    }
 
#else
 
    if (argc == 1)
    {
        Info << "Pass 'offline' or 'online' as first arguments."
             << endl;
        exit(0);
    }
 
    // process arguments removing "offline" or "online" keywords
    int argc_proc = argc - 1;
    char* argv_proc[argc_proc];
    argv_proc[0] = argv[0];
 
    if (argc > 2)
    {
        std::copy(argv + 2, argv + argc, argv_proc + 1);
    }
 
    argc--;
    // Construct the tutorial object
    tutorial02 example(argc, argv);
    tutorial02 FOM_test(argc, argv);
 
    if (std::strcmp(argv[1], "offline") == 0)
    {
        // perform the offline stage, extracting the modes from the snapshots'
        // dataset corresponding to parOffline
        offline_stage(example, FOM_test);
    }
    else if (std::strcmp(argv[1], "online") == 0)
    {
        // load precomputed modes and reduced matrices
        offline_stage(example, FOM_test);
        // perform online solve with respect to the parameters in parOnline
        online_stage(example, FOM_test);
    }
    else
    {
        Info << "Pass offline, online" << endl;
    }
 
#endif
    exit(0);
}
 
void offline_stage(tutorial02& example, tutorial02& FOM_test)
{
    // Read some parameters from file
    ITHACAparameters* para = ITHACAparameters::getInstance(example._mesh(),
                             example._runTime());
    int NmodesTout = para->ITHACAdict->lookupOrDefault<int>("NmodesTout", 15);
    int NmodesTproj = para->ITHACAdict->lookupOrDefault<int>("NmodesTproj", 10);
    // Set the number of parameters
    example.Pnumber = 9;
    example.Tnumber = 500;
    // Set the parameters
    example.setParameters();
    // Set the parameter ranges, in all the subdomains the diffusivity varies between
    // 0.001 and 0.1
    example.mu_range.col(0) = Eigen::MatrixXd::Ones(9, 1) * 0.001;
    example.mu_range.col(1) = Eigen::MatrixXd::Ones(9, 1) * 0.1;
    // Generate the Parameters
    example.genRandPar(500);
    // Set the size of the list of values that are multiplying the affine forms
    example.theta.resize(9);
    // Set the source term
    example.SetSource();
    // Compute the diffusivity field for each subdomain
    example.compute_nu();
    // Assemble all the operators of the affine decomposition
    example.assemble_operator();
    // Perform an Offline Solve
    example.offlineSolve();
    // Perform a POD decomposition and get the modes
    ITHACAPOD::getModes(example.Tfield, example.Tmodes, example._T().name(),
                        example.podex, 0, 0,
                        NmodesTout);
    // Perform the Galerkin projection onto the space spanned by the POD modes
    example.project(NmodesTproj);
    FOM_test.offline = false;
    FOM_test.Pnumber = 9;
    FOM_test.Tnumber = 50;
    // Set the parameters
    FOM_test.setParameters();
    // Set the parameter ranges, in all the subdomains the diffusivity varies between
    // 0.001 and 0.1
    FOM_test.mu_range.col(0) = Eigen::MatrixXd::Ones(9, 1) * 0.001;
    FOM_test.mu_range.col(1) = Eigen::MatrixXd::Ones(9, 1) * 0.1;
    // Generate the Parameters
    FOM_test.genRandPar(50);
    // Set the size of the list of values that are multiplying the affine forms
    FOM_test.theta.resize(9);
    // Set the source term
    FOM_test.SetSource();
    // Compute the diffusivity field for each subdomain
    FOM_test.compute_nu();
    // Assemble all the operators of the affine decomposition
    FOM_test.assemble_operator();
    // Perform an Offline Solve
    FOM_test.offlineSolve("./ITHACAoutput/FOMtest");
}
 
void online_stage(tutorial02& example, tutorial02& FOM_test)
{
    // Create a reduced object
    reducedLaplacian reduced(example);
 
    // Solve the online reduced problem some new values of the parameters
    for (int i = 0; i < FOM_test.mu.rows(); i++)
    {
        reduced.solveOnline(FOM_test.mu.row(i));
    }
 
    // Reconstruct the solution and store it into Reconstruction folder
    reduced.reconstruct("./ITHACAoutput/Reconstruction");
    // Compute the error on the testing set
    Eigen::MatrixXd error = ITHACAutilities::errorL2Rel(FOM_test.Tfield,
                            reduced.Trec);
}
//--------